Равномерное прямолинейное движение. Скорость Равномерным прямолинейным движением называют такое происходящее по прямолинейной траектории движение, при котором тело (материальная точка) за любые равные промежутки времени совершает одинаковые перемещения. Перемещение тела в прямолинейном движении обычно обозначают s. Если тело движется по прямой только в одном направлении, модуль его перемещения равен пройденному пути, т.е. |s|=s. Для того, чтобы найти перемещение тела s за промежуток времени t, необходимо знать его перемещение за единичное время. С этой целью вводят понятие скорости v данного движения. Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение: v=s/t. (1.1) Направление скорости в прямолинейном движении совпадает с направлением перемещения. Поскольку в равномерном прямолинейном движении за любые равные промежутки времени тело совершает равные перемещения, скорость такого движения является величиной постоянной (v=const). По модулю v=s/t. (1.2) Из формулы (1.2) устанавливают единицу скорости. В настоящее время в качестве основной системы единиц используют Международную систему единиц (сокращенно СИ - система интернациональная). Об этой системе рассказано далее. Единицей скорости в СИ является 1 м/с (метр в секунду); 1 м/с есть скорость такого равномерного прямолинейного движения, при котором материальная точка за 1 с совершает перемещение 1 м. Пусть ось Ох системы координат, связанной с телом отсчета, совпадает с прямой, вдоль которой движется тело, а x0 является координатой начальной точки движения тела. Вдоль оси Ох направлены и перемещение s, и скорость v движущегося тела. Из формулы (1.1) следует, что s=vt. Согласно этой формуле, векторы s и vt равны, поэтому равны и их проекции на ось Ох: sx=vx·t. (1.3) Теперь можно установить кинематический закон равномерного прямолинейного движения, т. е. найти выражение для координаты движущегося тела в любой момент времени. Поскольку х=x0+sx, с учетом (1.3) имеем х=x0+ vx·t. (1.4) По формуле (1.4), зная координату x0 начальной точки движения тела и скорость тела v (ее проекцию vx на ось Ох), в любой момент времени можно определить положение движущегося тела. Правая часть формулы (1.4) является алгебраической суммой, так как и х0, и vx могут быть и положительными, и отрицательными (графическое представление равномерного прямолинейного движения дано далее). Средняя и мгновенная скорости прямолинейного неравномерного движения Движение, при котором за равные промежутки времени тело совершает неравные перемещения, называют неравномерным (или переменным). При переменном движении скорость тела с течением времени изменяется, поэтому для характеристики такого движения введены понятия средней и мгновенной скоростей. Средней скоростью переменного движения vcp называют векторную величину, равную отношению перемещения тела s к промежутку времени t, за который было совершено это перемещение: vcp=s/t. (1.5) Средняя скорость характеризует переменное движение в течение только того промежутка времени, для которого эта скорость определена. Зная среднюю скорость за данный промежуток времени, можно определить перемещение тела по формуле s=vср·t лишь за указанный промежуток времени. Найти положение движущегося тела в любой момент времени с помощью средней скорости, определяемой по формуле (1.5), нельзя. Как указывалось выше, когда тело движется по прямолинейной траектории в одну сторону, модуль его перемещения равен пройденному телом пути, т.е. |s|=s. В таком случае среднюю скорость определяют по формуле v=s/t, откуда имеем s=vср·t. (1.6) Мгновенной скоростью переменного движения называют скорость, которую тело имеет в данный момент времени (и следовательно, в данной точке траектории). Выясним, каким способом можно определить мгновенную скорость тела. Пусть тело (материальная точка) совершает прямолинейное неравномерное движение. 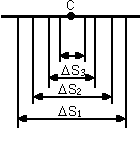Определим мгновенную скорость v этого тела в произвольной точке С ее траектории (рис. 2). Выделим маленький участок Ds1 этой траектории, включающий в себя точку С. Этот участок тело проходит за промежуток времени Dt1. Разделив Ds1 на Dt1, найдем значение средней скорости vcp1 =Ds1/Dt1 на участке Ds1. Затем для промежутка времени Dt2cp2 =Ds2/Dt2 на участке Ds21. Затем для промежутка времени Dt32 определим среднюю скорость vcp3 =Ds3/Dt3 на участке Ds3 и т.д. (участки траектории мы выбираем так, что точка С всегда находится внутри рассматриваемого участка). Очевидно, что чем меньше промежуток времени Dt, тем меньше длина участка Ds, проходимого телом, и тем меньше значение средней скорости vcp=Ds/Dt отличается от значения мгновенной скорости в точке С. Если промежуток времени Dt стремится к нулю, длина участка пути Ds бесконечно уменьшается, а значение средней скорости vcp на этом участке стремится к значению мгновенной скорости в точке С. Следовательно, мгновенная скорость v есть предел, к которому стремится средняя скорость тела vcp, когда промежуток времени движения тела стремится к нулю: v=lim(Ds/Dt). (1.7) Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю (если этот предел существует), представляет собой первую производную этой функции по данному аргументу. Поэтому формулу (1.7) запишем в виде v=(ds/dt)=s' (1.8) где символы d/dt или штрих справа вверху у функции обозначают производную этой функции. Следовательно, мгновенная скорость есть первая производная пути по времени. Если аналитический вид зависимости пути от времени известен, с помощью правил дифференцирования можно определить мгновенную скорость в любой момент времени. В векторной форме v=(ds/dt)=s'. Равноускоренное прямолинейное движение. Ускорение Такое прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, называют равноускоренным прямолинейным движением. Быстроту изменения скорости характеризуют величиной, обозначаемой а и называемой ускорением. Ускорением называют векторную величину, равную отношению изменения скорости тела v-v0 к промежутку времени t, в течение которого это изменение произошло: a=(v-v0)/t. (1.9) Здесь V0 - начальная скорость тела, т. е. его мгновенная скорость в момент начала отсчета времени; v - мгновенная скорость тела в рассматриваемый момент времени. Из формулы (1.9) и определения равноускоренного движения следует, что в таком движении ускорение не изменяется. Следовательно, прямолинейное равноускоренное движение есть движение с постоянным ускорением (a=const). В прямолинейном равноускоренном движении векторы v0, v и а направлены по одной прямой. Поэтому модули их проекций на эту прямую равны модулям самих этих векторов, и формулу (1.9) можно записать в виде a=(v-v0)/t. (1.10) Из формулы (1.10) устанавливается единица ускорения. В СИ единицей ускорения является 1 м/с2 (метр на секунду в квадрате); 1 м/с2 - это ускорение такого равноускоренного движения, при котором за каждую секунду скорость тела увеличивается на 1 м/с. Формулы мгновенной и средней скоростей равноускоренного движения Из (1.9) следует, что v= v0+at. По этой формуле определяют мгновенную скорость v тела в равноускоренном движении, если его начальная скорость v0 и ускорение а известны. Для прямолинейного равноускоренного движения эту формулу можно записать в виде v=v0+at. (1.11) Если v0 =0, то v=at. (1.12) Получим выражение для средней скорости прямолинейного равноускоренного движения. Из формулы (1.11) видно, что v=v0 при t=0, v1=v0+a при t=1, v2=v0+2a=v1+a при t=2 и т. д. Следовательно, в равноускоренном движении значения мгновенной скорости, которые тело имеет через равные промежутки времени, образуют такой ряд чисел, в котором каждое из них (начиная со второго) получается путем прибавления к предшествующему постоянного числа а. Это значит, что рассматриваемые значения мгновенной скорости образуют арифметическую прогрессию. Следовательно, средняя скорость прямолинейного равноускоренного движения может быть определена по формуле vср=(v0+v)/2, (1.13) где v0 - начальная скорость тела; v - скорость тела в данный момент времени. Уравнение равноускоренного прямолинейного движения Найдем кинематический закон прямолинейного равноускоренного движения. Для этого используем формулы (1.6), (1.11) и (1.13). Из них следует, что s=vср·t=(v0+v)·t/2=(2v0+at)·t/2, следовательно, s=v0·t+at2/2. (1.14) Если начальная скорость тела равна нулю (v0=0), то s=at2/2. (1.15) По формулам (1.14) и (1.15) определяют путь, пройденный телом в равноускоренном прямолинейном движении (модуль перемещения тела, не изменяющего направления своего движения). Для случая, когда тело движется по оси Ох. из точки с координатой х0, из формулы (1.14) получаем уравнение, выражающее зависимость координаты этого тела от времени. Поскольку x=xo+sx, а sx=v0x·t+axt2/2, имеем х=x0+v0x·t+at2/2. (1.16) Формула (1.16) есть уравнение прямолинейного равноуско-ренного движения (кинематический закон этого движения). Следует помнить, что в формуле (1.16) v0x и аx могут быть как положительными, так и отрицательными, так как это проекции векторов v0 и а на ось Ох. Связь перемещения тела с его скоростью Установим связь модуля перемещения s тела, совершающего равноускоренное прямолинейное движение, с его скоростью. Из формулы (1.10) находим, что t=(v-v0)/a. Подставив это выражение и формулу (1.13) в формулу (1.7), получим s=[(v0+v)/2]·[(v-v0)/a], следовательно, s=(v2-v02)/(2а) или v2=v02+2as. (1.17) Если начальная скорость тела равна нулю (v0=0), то v2=2as.