Резонанс
Резонансом принято называть явление резкого усиления отклика динамической системы x на внешнее воздействие f=f0coswt, когда частота внешнего воздействия w сравнима с собственной частотой w0 системы, либо с совокупностью частот собственных колебаний системы (nw=?niw0i, где n, ni целые числа). При этом вынужденные колебания x возникают и поддерживаются в системе за счет внешних аддитивных, либо параметрических воздействий (входящих в уравнения движения аддитивно, либо меняющих параметры системы). В последнем случае колебания, обусловленные внешним воздействием, называются параметрическими.
Колебания переменной x происходят с запаздыванием: при малых w<>w0 в противофазе (- ) с f (x~ - f0cos t/ 2); = 0 сдвиг фаз между колебаниями x и внешним воздействием - /2, а амплитуда колебаний x имеет наибольшую величину fQ/ 02, где Q= 0/ r - добротность системы при резонансе, а r - ее диссипация.
Заметим, что если динамическая система неавтономна, т.е. в уравнениях движения присутствует явная зависимость от времени, то такую систему можно рассматривать как автономную, введя время в качестве одной из координат фазового пространства. При таком подходе систему, описываемую дифференциальным уравнением второго порядка с внешним воздействием, можно рассматривать как систему с полутора степенями свободы.
Интересно отметить, что история развития физики началась фактически с исследования нелинейных уравнений - знаменитой задачи Кеплера. Задача Кеплера содержит типичные атрибуты нелинейной колебательной системы с параметрическим резонансом: зависимость периода обращения планеты вокруг Солнца от параметров орбиты, большое число гармонических составляющих во временных характеристиках текущих координат планет.
Последующее развитие теоретической и экспериментальной физики пошло по пути построения линейных физических теорий: теория упругости, электромагнетизм, задачи удержания тел и частиц вне зон параметрического резонанса, квантовая механика и квантовая теория поля. Понадобилось достаточно много времени (с XVII по XX век) [1 146], чтобы стало понятным: идеи линеаризации [1, 2, 4, 6, 13] абсолютно неприменимы для решения многих проблем, с которыми физика постоянно сталкивалась. И в этом смысле сегодня наблюдается возврат к классике.
Исторически одними из первых были рассмотрены задачи для линейных динамических систем с 0=const и с 0= 0{ i( t)} типа 0 =( o + 1cos t). Линеарилизация задач привела к "выплескиванию ребенка вместе с водой" - к отсутствию устойчивых состояний движения в зонах резонанса [4 7, 21 27].
Позднее были рассмотрены задачи параметрического резонанса с 0= 0f{ i(xk, ?l, t)}, где xk, ?l трансляционные и вращательные степени свободы, k, l = 1,2, 3N, N - количество степеней свободы [74 84, 95 97, 112 114, 122, 129, 146].
Задачи по изучению движения и удержанию различных частиц, клеток, тел с размерами от микро- до макро- с учетом их характеристик (зарядов, механических, электрических, магнитных моментов, массы) в неоднородных полях имеют почтенную историю и относятся к типичным задачам параметрического резонанса. Это обусловлено тем, что данная проблема периодически возникала при решении различных прикладных задач в различных областях механики, физики, биологии и медицины.
Отметим лишь некоторые из них:
а) роботизация пространственное бесконтактное ориентирование, удержание и управление микродеталями при сборке различных устройств, изделий и приборов;
б) селективная сепарация различных порошков (магнитных, ферромагнитных и т.д., в частности для магнитных носителей информации магнитные диски, ленты);
в) сверхчувствительные датчики полей (электромагнитных, акустических, гидродинамических, гравитационных) на основе подвесов;
г) взвешивание, удержание и перемещение различных тел (роторов двигателей, гироскопов, игрушек, транспорта на магнитном подвесе);
д) создание ловушек частиц различного типа с размерами от элементарных до макро- и изучение свойств, динамики отдельных частиц в таких ловушках, включая клетки, электроны, ионы, атомы, молекулы (с дальнейшей их упаковкой на плате - молекулярная технология), электродинамическое удержание плазмы;
e) получение автономных, устойчивых, осциллирующих систем, в частности самоустойчивой плазмы, активированной воды.
Решение подобного класса задач даже в первом приближении наталкивается на серьезные математические и физические проблемы.
Основная физическая проблема состояла в том, что в области взвешивания частиц при отсутствии источников поля (электрического, магнитного, гравитационного) могут существовать единственно особые точки седловые. Соответственно для седловых точек в одном направлении частица будет втягиваться в область взвешивания, а в другом выталкиваться. Данная проблема рассматривалась еще Гильбертом (1600) и Ирншоу (1842). Ими был установлен факт неустойчивости равновесия (статической магнитной конфигурации). В статике устойчивое удержание частицы согласно теореме Ирншоу просто невозможно [1].
Вывод о нестабильности равновесия уточнил Браунбек [2]. Он показал, что нестабильное равновесие в статике может стать устойчивым в динамике при наличии в системе диамагнитного тела. Однако в связи со слабым проявлением диамагнетизма у обычных веществ (за исключением сверхпроводников) результаты Браунбека не получили широкого практического распространения.
Но то, что запрещено в статике, может оказаться разрешенным в динамике (в переменных полях, либо при движении самих частиц в неоднородных полях).
В динамике же решение задач в свою очередь наталкивается на многочисленные математические проблемы. Основная проблема состоит в отсутствии общей теории колебаний сильно нелинейных систем при отсутствии малого параметра и в появлении "странных" особенностей даже при рассмотрении достаточно простых модельных систем, таких как аттрактор, хаос [3].
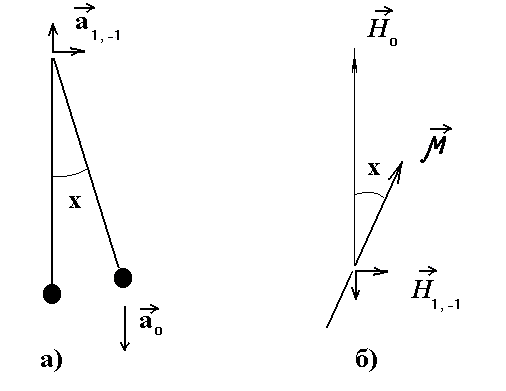
Как правило, в качестве "простой" модельной системы вынужденных колебаний с аддитивным и параметрическим воздействием рассматривается маятник с вибрирующей точкой подвеса. Это обусловлено тем, что соответствующее уравнение:
x '' + ?rx ' + (?0 + ?1cos )sin x - ?-1cos(?+?) cos x = 0, (1)
довольно часто встречается в различных областях физики: механике, электродинамике, физике плазмы и т.д. [3-18]. В частности, для маятника =( / )2; =(a /l)1/2; =0, 1, где ao=g ускорение силы тяжести, a1,-1 =l1,-1 ускорение при продольной, поперечной вибрации, частота вибрации, l длина маятника, l1,-1 амплитуды колебаний точки подвеса маятника (рис.1a). Для частицы с собственным магнитным моментом (рис.1б), 2= H /I, где I момент инерции, H0 напряженность постоянного магнитного поля, H1,-1 амплитуда переменного магнитного поля продольной, поперечной накачки, =const, ?= wt, x '=dx/d? .
|



